まず、磁場の変化から電場が生じる場合(電磁誘導)について、現在の方程式は妥当であるものと思われます。磁石のN極をコイルに近づけると、右ねじの回転する方向とは逆向きの電流が流れることから、$-\frac{∂B}{∂t}$ の符号は物理現象と一致しています。
また、電流から磁場が生じる場合の項 $μ_{0}J$ も、右ねじの回転する方向と磁場の向きが同じであることから、その符号(プラス)は物理現象と一致しています。
問題となるのは、電場の変化から磁場が生じる場合の項、すなわち $μ_{0}ε_{0}\frac {∂E}{∂t}$ の符号が正しいかどうかです。現在のマクスウェルの方程式ではプラスですが、対称性と実験結果の両面から見ると、ここには再検討の余地があるように感じました。
私は、次のように簡単な実験を行いました。
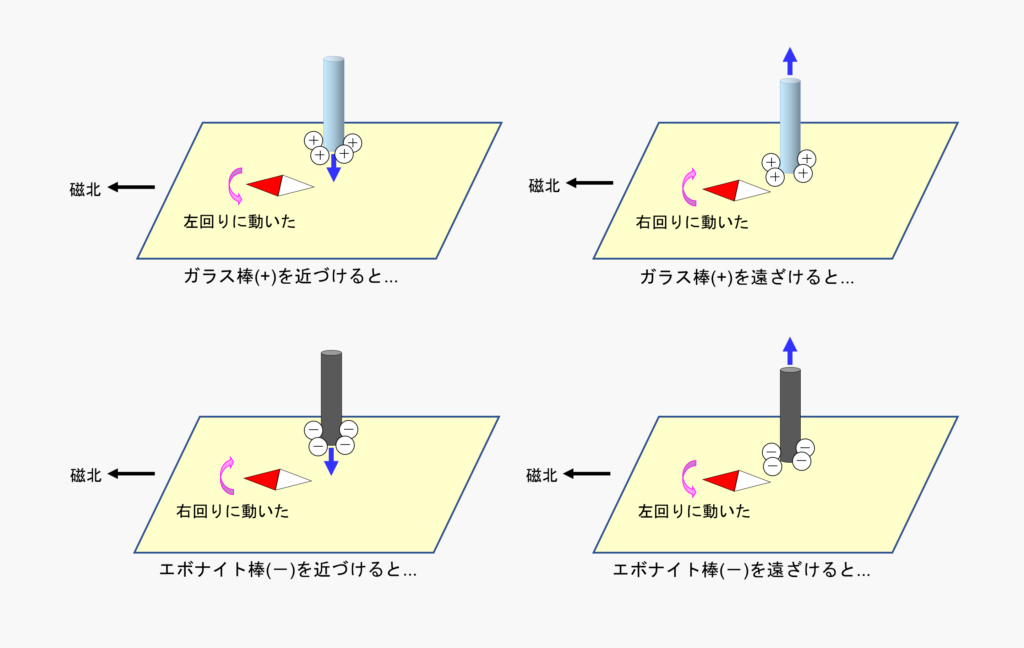
プラスに帯電したガラス棒、または、マイナスに帯電したエボナイト棒を用意しました。次に、それらを方位磁針に近づけたり、遠ざけたりして、電場の変化による磁場の動きを観察しました。
その結果、電場が増加する方向に対して、右ねじの回転方向とは逆の方向に磁場が生じることが明確に観測されました。これは、$μ_{0}ε_{0}\frac {∂E}{∂t}$ の符号(プラス)とは逆の現象です。
さらに、数値的な検討を行ったところ、$\frac {∂E}{∂t}$ の係数は $μ_{0}ε_{0}$ の値である $\frac{1}{c^2}\approx1\times10^{-17}$ という極めて小さな値に対して、実験で得られる係数は 1 に近い値であることも分かりました。これは、実に17桁という大きな差異です。
