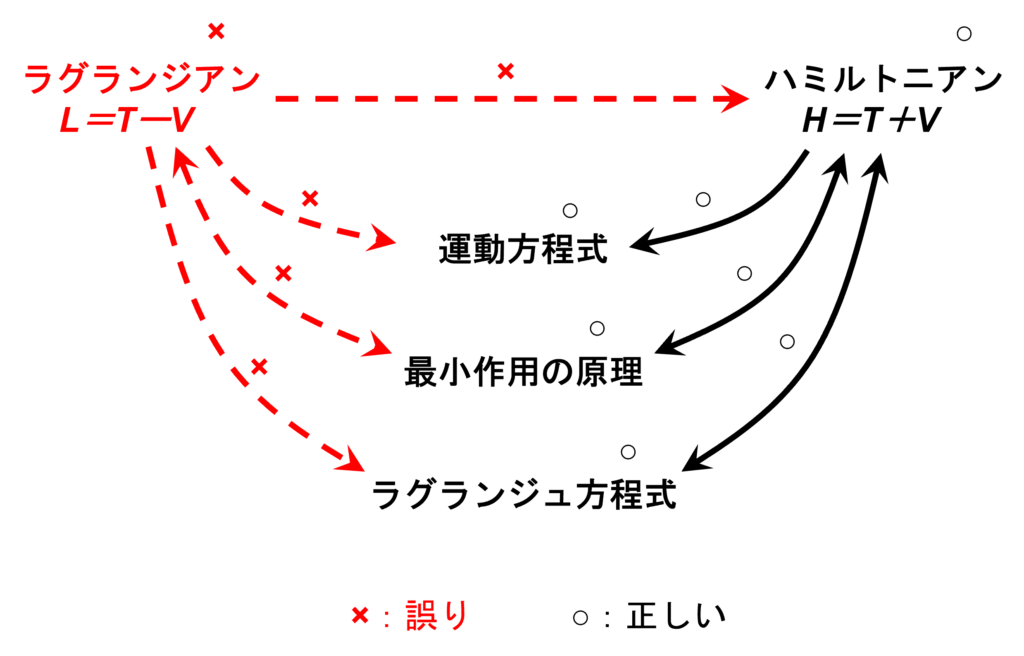
仮に、ラグランジアンの定義が本質的に「$T + V$」であると仮定した場合でも、従来の「$T – V$」という定義から導出された運動方程式が実際に正しかったことを考えると、「なぜ正しい結果が得られたのか?」という疑問が浮かびます。
これは、「マイナス同士を掛けるとプラスになる」現象として捉えることができます。数学では、マイナスの数とマイナスの数を掛けるとプラスの数になります。
具体的には、ラグランジアンの定義の符号が反転していても、ハミルトニアンなどの他の物理量を導出する過程で、もう一度ラグランジアンを適用すれば、マイナスの符号同士が打ち消されてプラスになるのです。
もちろん、これは一つの仮説であり、厳密な検証が必要な課題です。しかし、既存の定義体系の中に「偶然的な整合」が含まれている可能性を認識することは、新しい見方を提案するうえで有益かもしれません。